角運動量とは、物体の回転運動の特性です。
これは、物体が特定の点、または、軸の周りを回転し続ける傾向(本来数値で表すことのできない要素)を数値で表したものです。
簡単にいうと、回転の勢いを表す物理的な量で、どんな回転体も質量の中心周りに角運動量を持っています。
身近な例では、スケート選手のスピン、公園の回転遊具で見られ、この角運動量のおかげで地球も公転できているのです。
ここでは、角運動量について、身近な例をもとに、できるだけな言葉で紹介します。
身近な角運動量の例
例えば、公園にある回転遊具に乗っているとします。

乗り物がスピードを上げていくと、ハンドルを握る力が強くなっていくのを感じるでしょう。
これは、外側に押し出されるような感覚のためです。
では、この感覚の原因は何でしょうか?
別の例を挙げましょう。テレビでアイススケーターが様々なスタントやトリックを披露するのを見たことがあるかもしれません。
彼らの動きの一つに、高速で回転するものがあります。
最初は両腕を広げていますが、その後、腕を体に引き寄せてから閉じると、頭がくらくらするほど高速で回転し始めることに気づいたかもしれません。

これらの例はどちらも、角運動量の仕組みに関係しています。
簡単に言うと、角運動量とは、点、または、軸の周りを回転、または、自転する物体に含まれる回転運動の尺度です。
計算方法

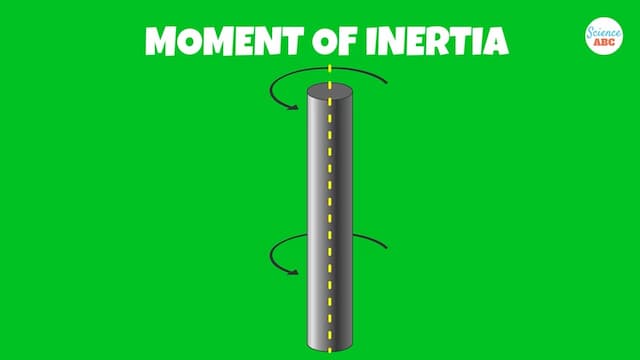
角運動量は、物体の「慣性モーメント(物体がどれだけ回転しにくいかを示す)x角速度(物体がどれだけ速く回転しているか)」として計算されます。
これは直線運動、または、直線で移動する物体に適用される線運動量に似ています。
数式も線形運動量の数式と似ていますが、線形運動量は「物体の質量x速度」です。
繰り返しますが、角運動量は、物体の慣性モーメントと角速度の積です。
慣性モーメント(回転しにくさ)は、回転質量としても知られ、回転軸に対する質量の分布を示します。
ここで、角運動量はベクトル量であり、「大きさ」と「向き」の両方あわせ持つ量であることに注意することが重要です。
角運動量はベクトル量
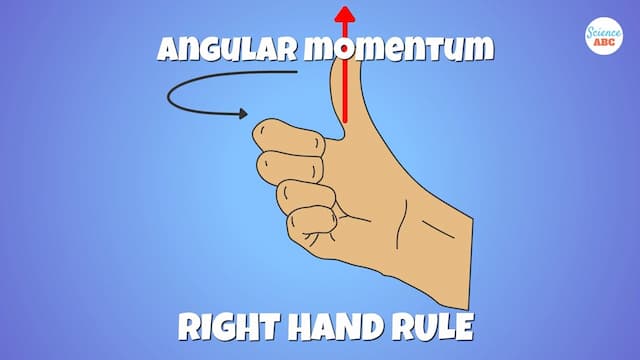
角運動量のベクトルは、右手の法則によって決定されます。
4本の指を物体の回転方向に向けたら、親指で3次元空間における角運動量のベクトル方向を示すことになります。
角運動量に関するもう1つの重要なことは、外部トルクが適用されない場合、閉鎖系の全角運動量は一定であるということです。
これをもう少し詳しく見てみましょう。
外部の力が影響しないとき角運動量は保存(一定に保たれる)

外部からの力がまったく影響を与えない場合、そのシステムは閉鎖系と呼ばれます。

1つ、または、複数の物体で構成される閉鎖系では、全角運動量は、そのシステム内のすべての個々の物体の角運動量の合計に等しくなります。

外部からこのシステムに影響を与えるものがない場合、つまり、何か外的要因が作用しない限り、全角運動量は変化せず、その値は維持されます。
これは角運動量保存の法則として知られています。
角運動量保存の法則は、日常生活で数多くの実用的な応用があります。
先に述べたアイススケーターを例に考えてみましょう。
アイススケーターが開いた腕を閉じると、他に大きな力が作用していないため、慣性モーメントが減少します。
このとき、角運動量は保存されたままで、回転速度が上昇します。
そのため、スケーターは回転軸の周りに質量を一時的に再分配することで、回転速度を上げることができます。
飛び込み台から飛び降りる水泳選手を考えてみましょう。

飛び降りた直後、選手は回転を始めたり宙返りをしたりすることがあります。
これにより体がコンパクトになり、慣性モーメントが減少します。

その結果、回転速度が上昇し、一時的に回転速度が速くなります。
ただし、水面に触れる直前に、ダイバーは腕と脚を伸ばすため、慣性モーメントが増加します。

これにより回転速度は低下しますが、全角運動量は保存されたままなので、通常よりも比較的ゆっくりと水面に着水します。
この法則は、私たちの宇宙の巨大な天体にも当てはまります。
角運動量のおかげで地球は公転できる
たとえば、私たちの太陽系の惑星は、楕円軌道を描いて太陽の周りを公転しています。
軌道上で太陽に比較的近づくと、惑星の速度が上がります。
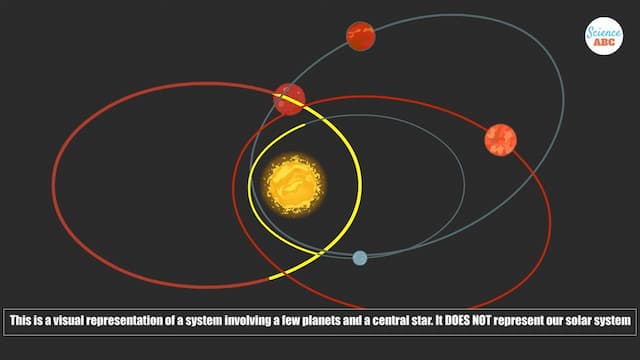
これは、太陽に近づくと惑星の慣性モーメントが低くなり、角運動量を一定に保つために速度が上がるためです。
太陽系は、誕生したときの回転運動の勢いが失われずに保たれていることで、その勢いを受け継いだ惑星が太陽の周りを楕円軌道で周り続けているのです。

量子システムでは、特に原子や分子において、角運動量は量子状態を定義する上で重要な役割を果たしています。
角運動量の量子化は原子軌道の構造に根本的に関わっているのです。
つまり、公園の回転遊具もフリスビーも、フィギュアスケーターの滑らかな回転も、恒星を公転する惑星や円運動する粒子も、宇宙全体で運動、力、回転をエレガントに結びつける物理学の基本原理である角運動量が作用しているのです。
角運動量については以下の動画で見ることができます。
