ある日、当時７才のガウスの学校の先生であるJ.G.ブトナーが、クラスのみんなにに算数の問題を出しました。
1時間で1から100までの数字をすべて足すという課題でした。
すぐに、ほとんどの生徒が、石板の上で数字を1つずつ足し始めました。しかし、ガウスは何も書きませんでした。彼は1分もたたないうちに答えを書いたのです。
他の生徒はみな忙しく足し算を続けました。1時間が経った後、バトナーは生徒の石板をチェックし、ガウスの結果が正しいのに気づきます。101の集まりが50個
小学生がどうやってその問題をあんなに早く解くことができたのでしょうか？
みなさんは分かりますか？以下にガウスの子供時代の逸話をもとに紹介します。
101の集まりを50個つくった
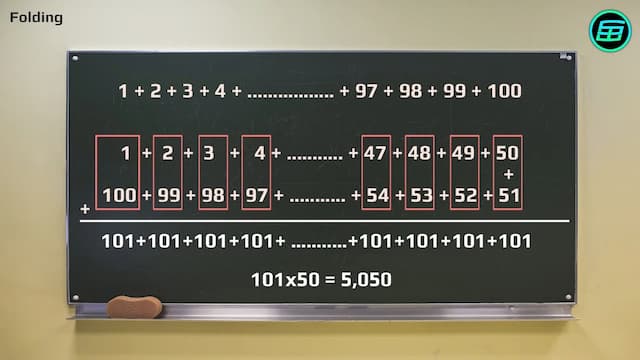
一部の研究者は、ガウスがこのように101の数字をつくって計算したと考えています。
図のように数字を縦に合計すると、すべて同じ結果「101」になります。
この101になる数字が50個あるので、結果は「101 x 50 ＝ 50050」に。
これは等差級数の和の公式として知られていますが、それをもし7才の子供がすでに自力でマスターしていたとなると驚きですね。
100までの数を2つつくる計算方法
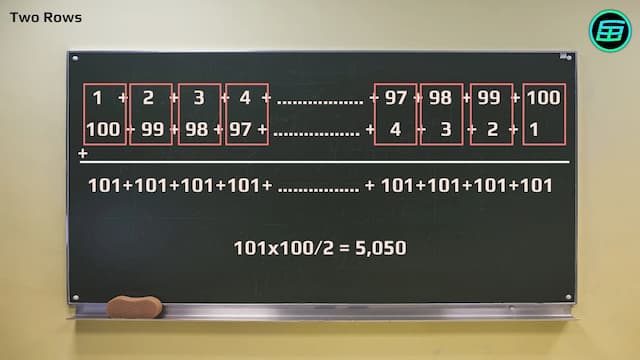
他の研究者は、ガウスが最初の1から順にその数の下に逆の順序（100から順に）で書き、前と同じように縦に数字を足して、101が合計100個分あるので、101×100をした後に2で割った（後から足した100までの数）「（101 x 100）÷ 2 = 5050」 と考えたのではないかと示しました。
るいは、平均化を用いたのかもしれません。
平均化で計算
最初の数と最後の数（100と1,99と2…）を順に足した後、それを2で割ると、平均50.5がでるため、100個分を50.5倍すると、答えは5050になります。
ガウスが実際にどの方法を使用したかはわかりませんが、この話は、数学や科学の問題は、適切なアプローチを見つけることができれば、はるかに簡単に解決したり理解したりできるという一般的なポイントを示しています。
ガウスの幼少期からの逸話
1855年に彼が亡くなった後、ガウスの友人で地質学者のヴォルフガング・ザルトリウス・フォン・ヴァルターハウゼンが彼の伝記を執筆しました。
ヴァルター・ハウゼンは、ガウスが幼い頃から並外れた知力を示し、家族に文字の音を尋ねることで読み方を学び、話す前に数の計算を覚えたといいます。
ヴァルター・ハウゼンによると、ガウスは3歳の時に父親の事業用帳簿の間違いを訂正しました。
15歳の頃には、毎日1000ずつ自然数に何個素数が現れるかを調べ、ガウスの死後にフランス人によって発表される「素数定理（自然数の中に素数が含まれている割合）」をすでに誰から学ぶこともなく予想していたようです。
いかがでしょうか？今回は、数学のおもしろさを実感できる逸話でした。
ガウスの計算については、以下の動画で見ることができます。