円は360度ですが、なぜ10度や100度のようなシンプルな数ではないのか考えたことはありませんか?
実のところ、360はとても理想的な数値なのです。純粋に数学的な観点からは、10や100のような数にするともっと不便だったでしょう。
ご存知の通り、「360」という数字は、7を除く1から10までのすべての数字で割り切れます。
さらに、360には24の約数(360を割り切れる小さい素数)があります。
1、2、3、4、5、6、8、9、10、12、15、 18、20、24、30、36、40、45、60、72、90、120、180 、そして360。
これは、360の値になるまでの任意の正の整数の約数の最大値です。
実はこれは、円が360度である理由の1つにすぎません。
以下に、なぜ円は360度なのいかについて分かりやすく紹介します。
計算がしやすい

360の約数は、24個でした。
では、100の約数はいくつあるでしょうか?
1、2、4、5、10、20、25、50、100
100の約数は、9つしかありません。

数値が正の整数であり、それよりも小さい正の整数よりも 多くの約数をもつ場合、その数値は高度合成数と言われます 。
360未満の高度合成数(自然数で、それ未満のどの自然数よりも約数の個数が多いもの)は、2、6、12、60、そして120だけです。
たとえば、360 は2つ、3つ、4つの部分に分割でき、結果の数は整数の180、120、90 です。
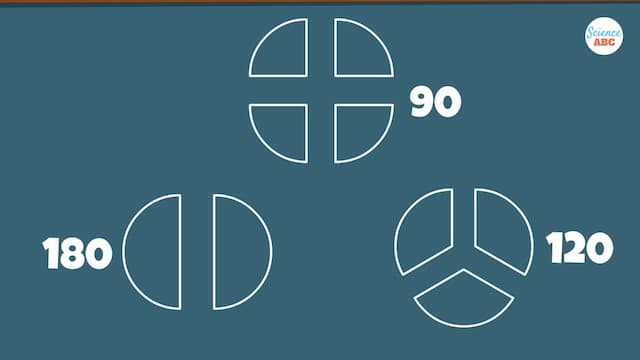
ただし、100を3で割っても整数にはなりません。

代わりに、33.3 という10進数の値が繰り返されるため、計算がはるかに難しくなります。
つまり、360を使用した計算は、慣れればとても簡単なのです。
バビロニア人の60進法に由来
完全な円が360度である理由として、バビロニア人に由来する1つの理論があります。
現在使用されているシステムは10進法と呼ばれ、基数が10で、0から9までの前の数字の)記号を繰り返して、新しい数字を形成します。

しかし、シュメール人とバビロニア人は、数字を形成するために60の異なる記号を持つ60進法を使用していました。
なぜ彼らは60を使用したのでしょうか?
実は、60は360と同じように、最大12の因数を持つ高度合成数だからです。
十進法で指で10を数えるのと同じように、右手の4本の指 (親指以外) の関節(各関節は3つずつある)を数えることから始めて、

「片手で12まで数え終わったら左手の1本を出す」を繰り返すと左手の5本指分をあわせて両手で60まで数えることもできます。

できあがる数は、右手の指の関節12本×左手の指5本=60本です。
一辺の長さが円の半径に等しい正三角形を描き、その頂点の1つを円の中心に置くと、合計6つの正三角形を円の中に収めることができます。

バビロニア人は60進法を使用していたため、各三角形の頂点は60度であると考えていました。

したがって、三角形6個 x 頂点60度からも360の値が得られます。
このようにして、さまざまな幾何学的応用や歴史的記録において、360という数字は便利で強力なツールであったようです。
以下は、なぜ円が360度なのかを紹介した動画です。
