実は、私たちが長さの単位に使う「メートル法」は完ぺきではありません。
そもそも、なぜ1メートルは今の長さなのでしょうか?もっと大きな数値ではいけないのでしょうか?
一定の速度で一直線に伝わる「光の速さ」は、誰が測っても常に一定なので、長さの基本単位の基準となったのです。
しかし、その定義にいたるまで、世界は多くの犠牲を生みました。
標準的な単位「メートル」が無い時代、人々はごまかしに満ち、不正し放題だったのです。
以下に、「標準メートル」がなぜ、どのようにして生まれたのかを興味深い時代背景とともに紹介します。
長さの単位が必要となった理由
1789年 フランスの国民は王政に不満を持っていましたが、そのなかには度量衡制度(長さや体積、重さの基準)への改善要求も含まれていました。
なぜなら、どの町や商人も、基本的に自分たちの都合がいいように物事を測っていたからです。
たしかに、古代エジプトの長さの単位は人の腕の長さでしたし、イギリスのインチは大麦3粒を端から端まで敷き詰めた長さで、人の歩幅を1メートルとする国もありました。
信じられないかもしれませんが、当時のフランスでは、1ポンドのパンが1ポンドの鉛より軽いことすらあったのです。それほど測量に関してはあいまいでした。
人々は25万種類もの尺度を使い分けていたわけですから、貿易は難しく、不正はいとも簡単に行われていたのです。
そこで、フランスの革命精神は、統一された平等な尺度を求めていきました。
そして、啓蒙主義者であるフランスの学者たちは、さらに高い目標を掲げたのです。
それは、世界で共通に使える統一した単位制度を作ることでした。
メートル法の基準
長さの基本単位は「メートル」と呼ばれ、他の(ミリやセンチ、キロなどの)長さの単位はすべてこのメートルから派生したものです。
そして、その単位は10進数で、ギリシャ語やラテン語の接頭辞をつけることで、歴史のある重要なものに聞こえるようにしました。
振り子の長さ説

まず最初に、基本となる「1メートル」に関しては、1秒間に1回振れる振り子の長さが、その1つの目安になりました。
当時、トーマス・ジェファーソンでさえこの測定に同意し、アメリカをこの新しい「メートル法」に参加させることにしたのです。
これで問題は解決したようにみえましたが、実際はそう簡単ではありませんでした。
まず、1秒の長さについて合意が必要でした。
フランスの学者たちは、私たちが使っている1日24時間、60分、60秒ではなく、10進法の1日(10時間、100分、100秒)に変えようと考えました。
残念ながら1秒の長さについて誰も合意できなかったので、振り子時計の考えは廃止されました。
(ちなみに、現在の一秒の単位は、1967年に「セシウム133原子が放射する波長」を基準に定義されています。)
地球上の距離を基準に定義
代わりに、フランスを通る子午線上の北極と赤道の距離の1千万分の1を1メートルとする考えが出されました。
しかし、イギリスとアメリカは、フランスを中心にした距離を受け入れることを拒否。
そこで1791年、2人の男(Ryan cosling、Channing Tatum)がメートル法を作ろうと本格的に動き出したのです。
その計画とは?

2つの緯度(51.03度と41.39度)を測り、真ん中で合流する位置を基準に出した数値。これなら距離と掛け算で出せます。
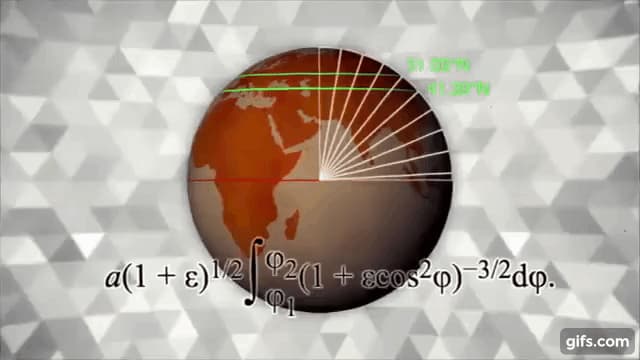
しかしこれには問題があり、1000kmも測れるはものさしが存在しないのです。
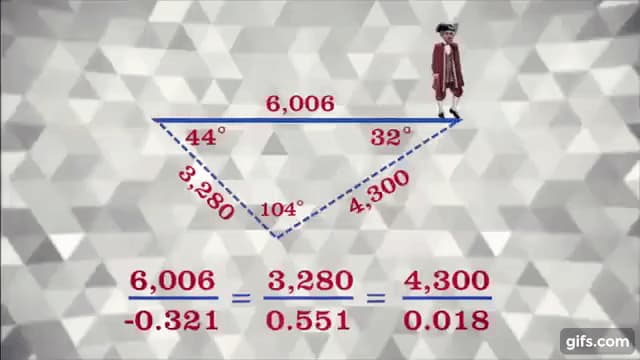
そこで、2つの地点を結ぶライン状に三角形の印をつけていき、三角形の一辺を南北にずらしながら、その角度をもとに鎖の長さを計算するという方法を思い立ったのです。
たしかに、これでは1回の測定で、ある程度の誤差が生じてしまいましたが、そのズレを計算で補正することで、これまでで最も正確な測量による、誤差の少ないメートル法を世に送り出せたのです。
ところが、この単位が始まるやいなや、フランスは革命や戦争の大混乱に陥ります。
三角形を作るときに、2地点間の角度を測るのに使われたのが環(わ)に2つの望遠鏡を通した装置でした。

街々で、人々はこのおかしな道具を持って計測する科学者を王室のスパイだと思い、そのたびに彼らは命の危険に晒されたといいます。
そして、7年間の闘争の末、彼らはようやく三角形を目標地点までつなげたのです。
1799年、何ページにもわたる計算が見直され、北極から赤道までの距離が決まり、その1千万分の1の長さを「1メートル」としました。
人類はついに、自然界から得た普遍的な尺度「標準メートル」を手に入れたように思えましたが、しかし、1つだけ問題がありました。それは、導き出された「1メートル」自体が間違っていたこと。
メートルを計算するためには、地球の曲率を正確に測定する必要があったのです。
ニュートン以来、地球の断面が円ではなく楕円であることは科学者たちの常識でした。
しかし、メートル探検の結果、地球は科学者が考えていたよりも2倍もつぶれていたのです。でも実際には2倍ではなく、ただ測定に不適切な線を選んだに過ぎなかったようです。しかも、その曲線は滑らかではありません。
たしかに地球の曲線が滑らかではないこと自体は大きな発見でしたが、同時に、測定器の前提が崩れることにもなりました。
「標準メートル」の誕生
結局のところ、地球は不規則すぎて、それ自体を測定することはできないのです。
今日、私たちは地球に基づいてメートルを測定しているわけではありません。
1960年、メートルは原子の波長数として再定義されましたが、これは古いプラチナ棒と一致するように計算されたものでした。
実のところ、地球の平均曲率を衛星で測定した結果、現在では極点から赤道までの1000万メートルは約2キロメートル足りないことが分かっています。
メートル法というのは完全な比率として発明されたものですが、光速を基準にした私たちの標準メートルでさえ、本来あるべき距離より10分の2ミリ短いという誤差があるのです。
実際に、光が直線で進む距離を基準に測定すると、月までの距離にも最大30cm程度の誤差は出るようです。
そうはいっても、私たちがそう言っているのだから、それはまだ1メートルなのでしょう。
メートル法は画期的な発明だった
メートルは物理的な物体ではありません。
メートル法は数学の問題なのです。
それは、物理学のまさに基礎に組み込まれた単位で、メートル法システムの基本単位です。
宇宙の基本法則の中で、メートルという単位がなぜメートルなのかを説明するものはありませんが、それでも発明としては画期的なものだといえるでしょう。
