列車の車輪は完全な円筒形ではなく、わずかに円錐形になっています。
そして、この円錐形の先を切り取ったような形は、2つの大きな偉業を達成した工学上の驚異と考えられています。
1つは、車輪の進路を中央に向けて自動で修正。
もう1つは、列車の差動動作を実現することです。これによって、列車は、レールの外側が内側よりも距離が長くなるカーブに対応して曲がることができるのです。
ここでは、車輪と車軸が一体になったものが、どうやって内側と外側で長さの違いがある線路を曲がれるのかを中心に分かりやすく紹介します。
円錐に近い形の理由
これを、2つの紙コップを使った簡単な実験で考えてみましょう。
2つの紙コップの上側を貼り付けて線路の上を転がすと、完全にまっすぐに動くのがわかります。

紙コップを少し傾けても、まっすぐに動きます。
では、このセットはどうでしょうか。これは底同士を付けています。

こちらは、先ほどと同じ線路上でどのような転がし方をしても常に失敗します。
実は、鉄道の車輪は先ほどの円錐形を使用しています。
この角度によって、車輪が線路から外れることがなくなるのです。
車輪の自律的な動きを促す
しかし、なぜこの円錐形の配置がこれほど効果的(自律中心化力を生み出す)なのでしょうか?
この仕組みを理解するには、まっすぐ進むときに車輪に働く力を確認する必要があります。
車輪が自律的に中心に向けて移動する理由
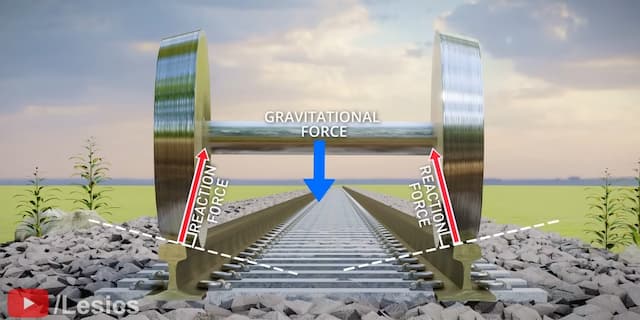
車輪に働く主な力は、重力、そして、反力(車輪が地面を圧する重力とつりあう同等の力が接地面から作用)。
反力は、常に車輪の接地面に対して垂直になります。
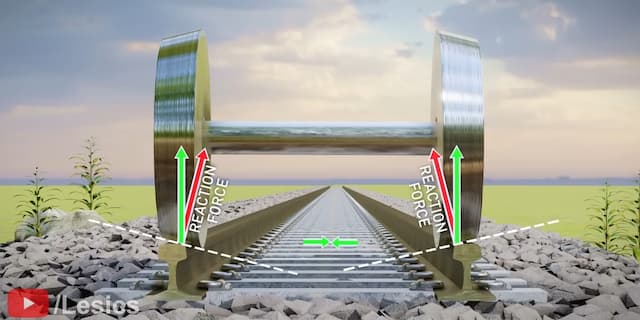
車輪がレールの中心にある場合、これらの力の水平成分は互いに打ち消されます。
ここで、何らかの理由で車輪が右に移動したとします。
車輪が軸に沿って移動すると、興味深いことが起こります。

図から明らかなように、車輪のセット全体が傾いています。
この傾きに合わせて、法線力(接地面に垂直に働く力)も傾きます。
この状態で力の解析を行うと、左方向への正味の力(NET FORCE:車輪に働く全ての力の大きさと向きをもつベクトルの和)がかかっていることがわかります。

この力は、右に寄った車輪を自律的に中心に移動させます。
車輪が中心に近づくと、自己中心化力は消えます。
これは、車輪が自律的に中心に移動するシンプルでありながら優れた手法です。
さらに、車輪が線路から外れないように安全機能のオプションとして、左右それぞれの車輪にはフランジと呼ばれる凸部が取り付けられています。


車輪が逆の形になったらどうなるのか?

さて、ここでちょっとおもしろいお話をしましょう。
列車の車輪が紙コップの底同士をつなげたような逆の形になったとします。
車輪が右に寄ったときにかかる先ほどのような力の解析を行うと、発生する正味の力も右方向になっていることがわかります。

これが、最初の紙コップの実験で、この車輪の形状では、車輪が常に線路から外れてしまう理由です。
内側と外側でのレールの長さの差に対応して曲がる仕組み
次に、車輪を円錐形にする2つ目の理由を探ってみましょう。
先ほどこの円錐形により、エンジニアは差動作用を実現できたと示しました。
通常、カーブでは、外側の車輪は内側より長い距離を移動する必要があります。

では両方が車軸つながっているはずなのに、なぜ一方の車輪がもう一方の車輪よりも長い距離を移動できるのでしょうか。
ここで円錐形が役に立ちます。
これを実現するために、カーブで車輪を回転させてみると、車輪は少しずつ左にスライドします。
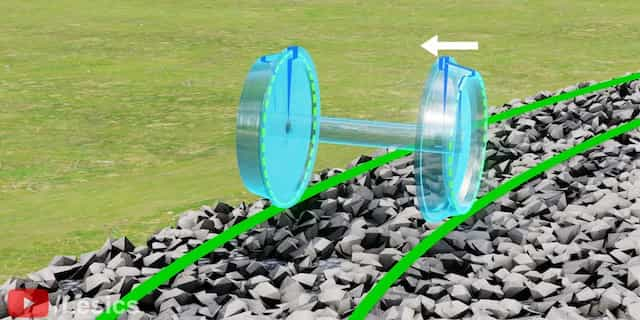
車輪の接地点をみると、左の車輪は右の車輪よりも半径が大きいことに気づきますか?
つまり、同じ角度で回転すると、左の車輪の方が長い距離を移動し、差動動作を実現しているのです。
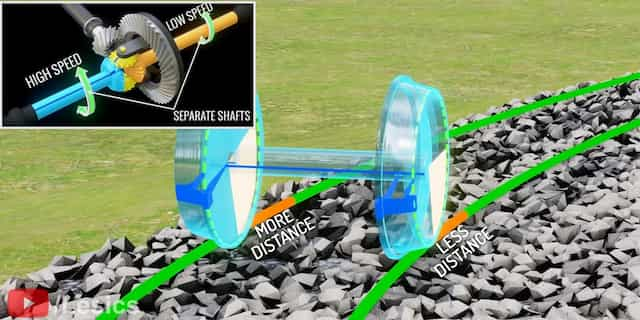
これを列車では、車輪に円錐形を与えるだけでこの差動動作を実現したのです。
興味深いですね。
もちろん、車輪が左にスライドすると、コーナリング中に先ほど見たように、右に向かう力が自動的に発生します。

この力は、列車がコーナーを曲がるのに必要な求心力を生み出しているのです。
これにより、曲がっている最中に車輪が中心に戻ることはありません。
このように車輪をわずかに円錐形に近づけるだけで、2つの主なエンジニアリング目標を達成することができるなんて本当に驚きですね。
